Getting started with Sum of Squares

Documentation and examples on using Sum of Squares solvers, tutorial and examples of Sum of Squares programming

Here is a list of exercises to be used during the AMS Short Course “Sum of Squares: Theory and Applications”.

Exercise 1

Consider the polynomial $p(x) = x^4 + 2 a x^2 + b$. For what values of $(a,b)$ is this polynomial nonnegative? Draw the region of nonnegativity in the $(a,b)$ plane. Where does the discriminant of $p$ vanish? How do you explain this?

Exercise 2

Let $M(x,y,z) = x^4 y^ 2+ x^2 y^4 + z^6 - 3 x^2 y^2 z^2$ be the Motzkin polynomial. Show that $M(x,y,z)$ is not SOS, but $(x^2+y^2+z^2) \cdot M(x,y,z)$ is.

Exercise 3

Give a rational certificate of the nonnegativity of the trigonometric polynomial $p(\theta) = 5 - \sin \theta + \sin 2\theta - 3 \cos 3\theta$.

Exercise 4

Consider a univariate polynomial of degree $d$, that is bounded by one in absolute value on the interval $[-1,1]$. How large can its leading coefficient be? Give an SOS formulation for this problem, solve it numerically for $d=2,3,4,5$, and plot the found solutions. Can you guess what the general solution is as a function of $d$? Can you characterize the optimal polynomial?

Exercise 5

Consider a given univariate rational function $r(x)$, for which we want to find a good polynomial approximation $p(x)$ of fixed degree $d$ on the interval $[-2,2]$.

Write an SOS formulation to compute the best polynomial approximation of $r(x)$ in the supremum norm.
Same as before, but now $p(x)$ is also required to be convex.
Same as before, but $p(x)$ is required to be a convex lower bound of $r(x)$ (i.e., $p(x) \leq r(x)$ for all $x \in [-2,2]$).
Let $r(x) = \frac{1-2 x+x^2}{1+x+x^2}$. Find the solution of the previous subproblems (for $d=4$), and plot them.

Exercise 6

Consider the polynomial system $\{ x+y^3 =2, x^2+y^2=1\}$.

Is it feasible over $\mathbb{C}$? How many solutions are there?
Is it feasible over $\mathbb{R}$? If not, give a Positivstellensatz-based infeasibility certificate of this fact.

Exercise 7

Consider the butterfly curve in $\mathbb{R}^2$, defined by the equation

\[x^6 + y^6 = x^2.\]

Give an sos certificate that the real locus of this curve is contained in a disk of radius $5/4$. Is this the best possible constant?

Exercise 8

Consider the quartic form in four variables

\[p(w,x,y,z) := w^4 + x^2y^2 + x^2z^2 + y^2z^2 - 4wxyz.\]

Show that $p(w, x, y, z)$ is not a sum of squares.
Find a multiplier $q(w,x,y,z)$ such that $q(w,x,y,z) p(w,x,y,z)$ is a sum of squares.

Exercise 9

Consider a random variable $X$, with an unknown probability distribution supported on the set $\Omega$, and for which we know its first $d+1$ moments $(\mu_0,\ldots,\mu_d)$. We want to find bounds on the probability of an event $S \subseteq \Omega$, i.e., want to bound $P(X \in S)$. We assume $S$ and $\Omega$ are given intervals. Consider the following optimization problem in the decision variables $c_k$:

\[\text{minimize} \sum_{k=0}^d c_k \mu_k \qquad \mbox{s.t.} \quad \begin{cases} \sum_{k=0}^d c_k x^k \geq 1 & \forall x \in S \\ \sum_{k=0}^d c_k x^k \geq 0 & \forall x \in \Omega. \end{cases}\]

Show that any feasible solution of this problem gives a valid upper bound on $P(X \in S)$. How would you solve this problem?
Assume that $\Omega = [0,5]$, $S = [4,5]$, and we know that the mean and variance of $X$ are equal to $1$ and $1/2$, respectively. Give upper and lower bounds on $P(X \in S)$. Are these bounds tight? Can you find the worst-case distributions?

Exercise 10

The stability number $\alpha(G)$ of a graph $G$ is the cardinality of its largest stable set. Define the ideal $I = \langle x_i (1-x_i) \quad i \in V, \quad x_i x_j \quad (i,j) \in E \rangle$.

Show that $\alpha(G)$ is exactly given by

\[\min \gamma \qquad \gamma - \sum_{i \in V} x_i \quad \text{is SOS mod $I$}.\]

[Hint: recall (or prove!) that if $I$ is zero-dimensional and radical, then $p(x) \geq 0$ on $V(I)$ if and only if $p(x)$ is SOS mod $I$.]

Recall that a polynomial is 1-SOS if it can be written as a sum of squares of affine (degree 1) polynomials. Show that an upper bound on $\alpha(G)$ can be obtained by solving

\[\min \gamma \qquad \gamma - \sum_{i \in V} x_i \quad \text{is 1-SOS mod $I$}.\]

Show that the given generators of the ideal $I$ are already a Gröbner basis. Show that there is a natural bijection between standard monomials and stable sets of $G$.
As a consequence of the previous fact, show that $\alpha(G)$ is equal to the degree of the Hilbert function of $\mathbb{R}[x]/I$.

Now let $G =(V,E)$ be the Petersen graph, shown below.

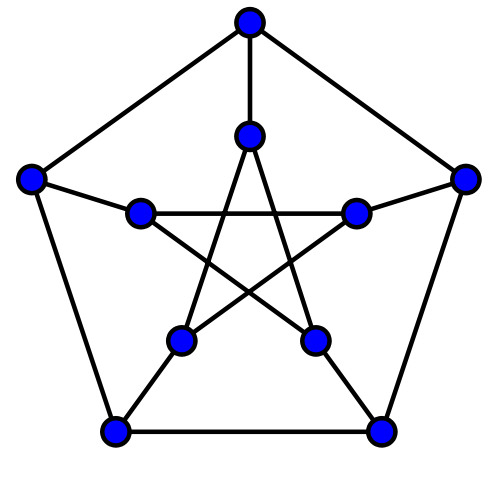
Find a stable set in the Petersen graph of maximum cardinality.
Solve this optimization problem for the Petersen graph. What is the corresponding upper bound?
Compute the Hilbert function of $I$ using Macaulay2, and verify that this answer is consistent with your previous results.

Exercise 11

Consider linear maps between symmetric matrices, i.e., of the form $\Lambda:\mathcal{S}^n \rightarrow \mathcal{S}^m$. A map is said to be a positive map if it maps the PSD cone $S^n_+$ into the PSD cone $S^m_+$ (i.e., it preserves positive semidefinite matrices).

Show that any linear map of the form $A \mapsto \sum_i P_i^T A P_i$, where $P_i \in \mathbb{R}^{n \times m}$, is positive. These maps are known as decomposable maps.
Show that the linear map $C:\mathcal{S}^3 \rightarrow \mathcal{S}^3$ (due to M.-D. Choi) given by:

\[C:A \mapsto \begin{bmatrix} 2 a_{11} + a_{22} & 0 & 0 \\ 0 & 2 a_{22} + a_{33} & 0 \\ 0 & 0 & 2 a_{33} + a_{11} \end{bmatrix} - A.\]

is a positive map, but is not decomposable.

Hint: Consider the polynomial defined by $p(x,y) := y^T \Lambda(x x^T) y$. How can you express positivity and decomposability of the linear map $\Lambda$ in terms of the polynomial $p$?

End of exercises.